Technological improvements and competition in the survey services industry have driven down the cost of LiDAR acquisition significantly in recent years. As a result of this, LiDAR is rapidly gaining popularity in the forest industry for a variety of applications, including road planning and design. The availability of this accurate topographic data is allowing engineers to design and plan forest operations before setting foot on the site. Traditional forest engineering workflows based on extensive preliminary field work are changing.
This article examines current road planning and design workflows using LiDAR, and outlines a workflow for determining road location, based on a new automated optimization software technology. Developed in collaboration with the University of British Columbia, this new technology generates the lowest cost road location (both horizontally and vertically) based on earthwork volume and movement costs, as well as constraints such as minimum grades and K values. Alignment optimization offers new opportunities to take advantage of LiDAR data and improve engineering workflow. The outlined change in workflow to include optimization ultimately reduces engineering time both in the office and in the field, and also reduces construction costs.
Introduction
Forest road construction is one of the most expensive components of timber harvesting. The selection and planning of roads is a difficult and time consuming task which can greatly influence the profitability of forest operations. In addition to the construction expenses, a poorly designed road may increase cycle times and vehicle maintenance costs.
Software tools which allow forest engineers to locate and design better roads has been a sought-after goal for many years (Akay 2003; Ghaffariyan et al. 2010; Reutebuch 1988; Rogers & Schiess 2001; Sessions 1992; Sessions 1978; Stueckelberger et al. 2006; Tan 1999). However, applying these tools to imprecise survey data renders them impractical. The increasing availability of high resolution ground information from sources such as LiDAR is removing this obstacle.
In Western Canada, LiDAR has been studied and used for forest engineering applications for more than 10 years (Ghaffariyan et al. 2010). In the last 2 years, the usage has increased significantly, largely due to reduced acquisition costs (D’Eon 2015). Studies have shown a payback of less than 2 years and a savings of $1.57/m3 harvested (D’Eon 2015). A web-based survey of 73 forestry companies in March 2015 indicated that 63% were using LiDAR for road planning, and 18% expected to be doing so in the near future (Softree 2015).
This paper introduces a new methodology for planning and designing forest roads using accurate LiDAR data and mathematical optimization software. We will examine the following:
- conventional workflows for route planning, survey, and road design;
- a new method for road design and cost estimation using mathematical optimization techniques; and
- improved workflows using LiDAR and optimization software to save field time, reduce construction costs, and lower road operating and maintenance costs.
Mathematical Optimization for Alignment Selection
Overview
Mathematical optimization techniques for forest road planning and design have been studied for more than 20 years. Various mathematical methods have been proposed, including genetic algorithms, network modelling, mixed integer programming, and simulated annealing (Akay 2003; D’Eon 2015; Reutebuch 1988; Rogers & Schiess 2001; Sessions 1992).
The two key motivations for using optimization are to:
- save planning and engineering time; and
- find lower cost, better alignments.
The first of these two motivations is probably the most tangible, and by itself may make the cost of the optimization software quite small in comparison with the savings.
Method
Our approach to optimization is to divide the problem into two sub-problems: vertical and horizontal optimization. In order to compare 2 different horizontal alignments, it is necessary to calculate their respective costs. This in turn requires the calculation of their optimal vertical alignments. The inputs to optimization are shown in Figure 1. These include existing ground, preliminary horizontal alignment, cross section geometry, costs, and constraints.
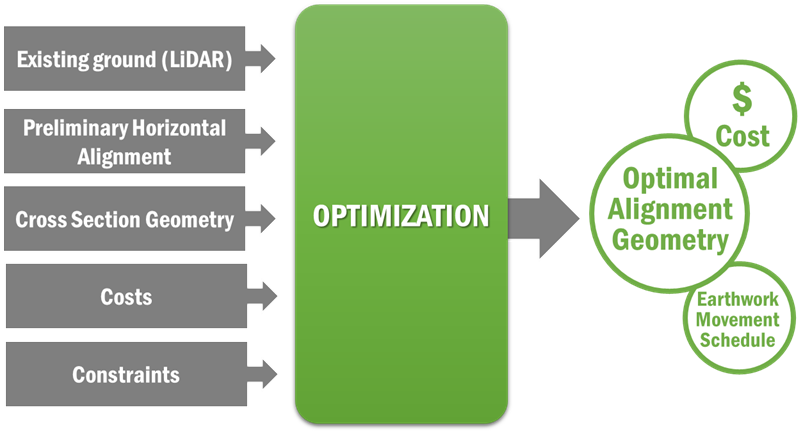
Figure 1: Optimization Process Overview
Cost Function
A variety of cost functions have been proposed, including maintenance costs, transportation costs, and environmental costs (Akay 2003; Sessions 1992).
Although the cost function is flexible, we have chosen to restrict its scope to minimizing earthwork costs. This not only makes the software easier to use, but also relieves the user from the difficult task of determining other less understood costs. Alignment costs can be compared, as shown in Figure 2. Costs within the scope of the cost function include:
1) cut / fill costs are considered for sub-grade and surfacing materials:
- cut cost [$ / Cu. m.] - cost to excavate by material (e.g. rock would be more expensive); and
- fill cost [$ / Cu. m.] - cost to embank or compact material into the road bed.
2) movement and loading costs:
- freehaul (shovel or dozer) movement [$ / (Cu. m. x km.)];
- endhaul (truck) movement [$ / (Cu. m. x km.)]; and
- endhaul loading [$ / Cu. m.].
3) additional costs:
- clearing and grubbing [$ / Sq. m.];
- culverts; and
- pit opening costs [$].

Figure 2: Cost Comparison Between 2 Alignments
Based on the cost function, the optimization process will calculate volumes, material movement (endhaul) and other costs, and will report the total cost for an alignment. As discussed later, this ability to quickly calculate the cost of an alignment is very useful in the early stages of planning.
It is also worth mentioning that, for the purpose of comparing alignments, the true construction unit costs are not necessary. Representative or typical unit costs will generally lead to selection of the best alignment alternative.
Constraints
Constraints are necessary to impose road standards such as design speed and maximum grades. Without constraints, the optimal solution would simply follow the ground balance line and the road would be un-driveable. The following constraints are available:
- min./max. grades by station range;
- min. K by station range;
- fixed control points (elevation and grade);
- full bench sections;
- min. fill height;
- min. cut depth; and
- material movement direction.
- cross sections displaying road width, cut / fill slopes, and surfacing depth;
- plan and profile views displaying vertical and horizontal alignment; and:
- location of field reference points (for example, private property boundaries);
- location, type and size of drainage structures;
- locations of special design sections (for example, retaining structures);
- locations and dimensions of turnouts;
- locations of landings, pits, quarries and spoil sites;
- sites of specific concern for construction;
- locations of endhaul sections; and
- clearing width.
- excavation and embankment volumes;
- probable material type (soil, rock, organic overburden, etc.);
- mass haul diagrams; and
- surfacing requirements, where applicable.
Borrow / Waste Sites
All cut / fill volumes must be accounted for in the optimization process. Steep slope forest roads, such as those found throughout British Columbia, usually have an excess of material to deal with. In situations where material cannot be placed back into the road bed or sidecast, it must be endhauled at considerable expense.
To determine the most economic way to handle materials, the optimization process needs to know of possible borrow, waste, and sidecast locations. The optimization software considers the site capacity, available materials, site opening cost, and distance from the main alignment in the determination of the optimal movement. Figure 3 shows a typical material movement.
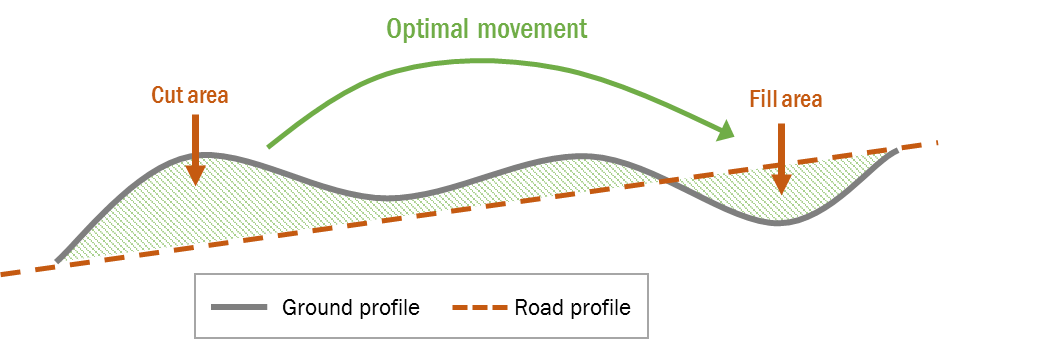
Figure 3: Typical Material Movement Optimization
Vertical Optimization
In the vertical optimization phase, an alignment is found which minimizes the cost of cutting, filling, and earth movement for each type of material (rock, overburden etc.). The user can impose constraints between different sections of the road such as grades, K values, or control points. A unique and innovative property of the method is the ability to accurately handle detailed cross sections, including ditches, variable side slopes, and rock cuts etc.
The vertical optimization model uses a mixed integer linear programming (MILP) method which solves relatively quickly and guarantees optimality. Although the handling of detailed cross sections and sophisticated constraints makes the problems complicated, it remains a deterministic optimization problem and is generally solvable using modern MILP solvers in a reasonable amount of time, often within minutes.
For vertical optimization, the horizontal alignment is fixed. Vertical optimization is restricted to a user-controlled vertical band. Cross sections are used to calculate areas and volumes.
Vertical optimization can be used to create an alignment from scratch or to refine an existing alignment. It can also be used to investigate the effect of changing design speed, grades and other parameters.
Horizontal Optimization
Finding an optimal alignment connecting two arbitrary end-points is a highly complex problem that requires solving three interrelated sub-problems, namely the horizontal alignment, vertical alignment and earthwork optimization problems. To reduce the complexity of the problem, we propose a solution which restricts the search space of the optimizer to a user-defined corridor, as shown in Figure 4, along with alignment candidates within the defined corridor.
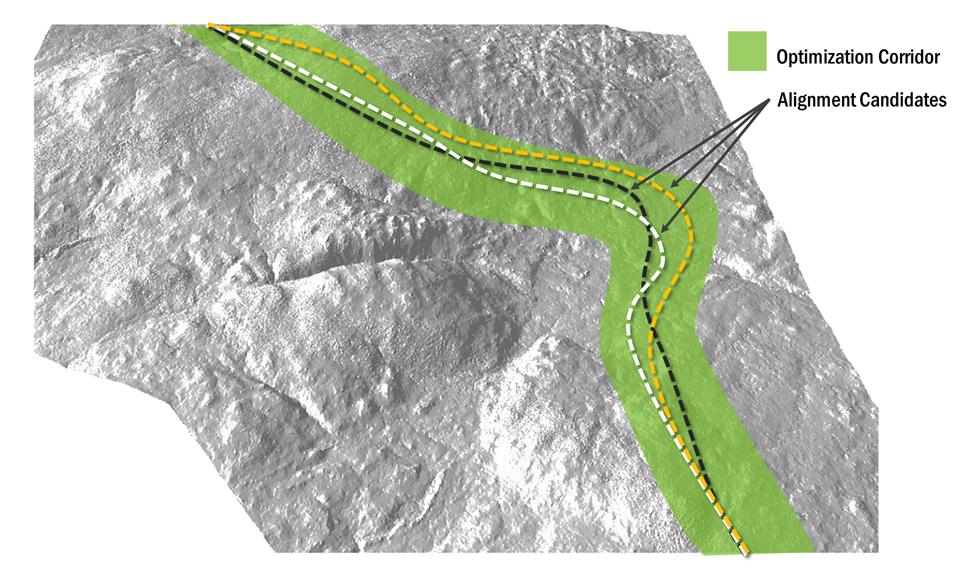
Figure 4: Horizontal Optimization within a Specified Corridor
Our approach is to use a bi-level optimization model combining these three problems. Figure 5 exemplifies a simplified bi-level optimization process. In the outer level of the model, the horizontal alignment is optimized, and in the inner level of the model a vertical alignment optimization problem considering earthwork allocation is solved for the fixed horizontal alignment. Derivative-free optimization algorithms are used to solve the outer problem (Conn et al. 2009).
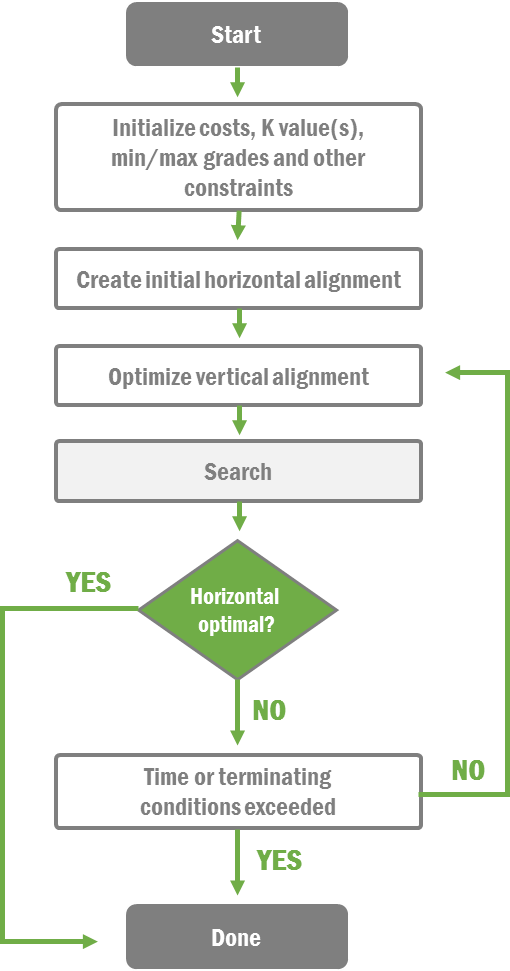
Figure 5: Horizontal Optimization Process Using Derivative-Free Optimization
Traditional Approach to Road Planning and Design
Traditional road planning generally consists of 3 phases: route selection, field verification and survey, and design and construction documentation, as shown in Figure 6 below.
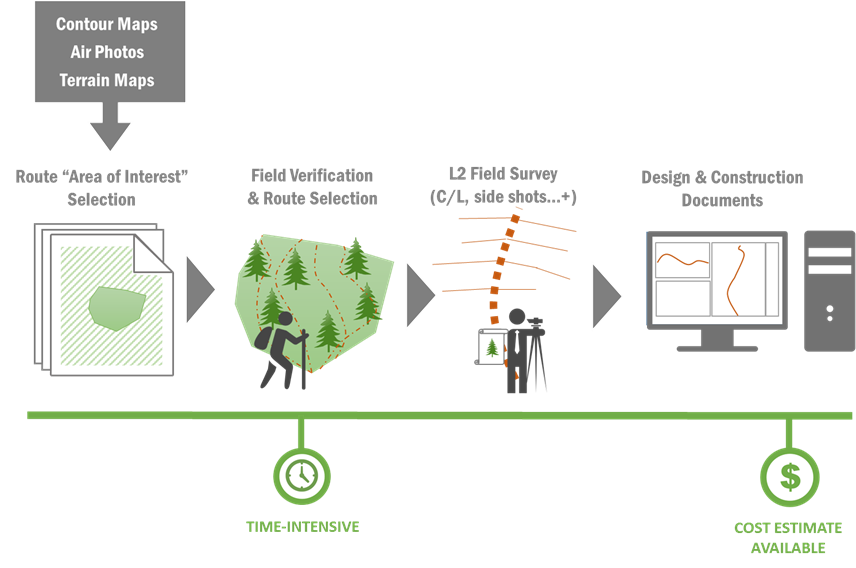
Figure 6: Traditional Workflow for Road Planning
Route Selection
Road planning is part of the overall planning process. It must consider the volume of timber to be transported, as this affects the overall financial investment. Decisions made during the route selection affect all other stages, and may have long-term effects on road construction and maintenance costs, user safety, and other resources.
Route selection for harvest planning usually commences with a review of air photos and terrain mapping. Without accurate ground information, computer-based design and cost estimation is not possible at this stage. This involves field work and extensive ‘ground truthing’. Selecting a proven try line involves evaluation of cuts and fills, which is done by eye and requires experience. The planner must rely on a working knowledge of the area to identify acceptable alignments and grades.
Field Verification and Survey
Once a suitable alignment has been identified, field verification and survey can begin. Collection of field information is labor intensive and time consuming. In difficult terrain, or when good topographic map information is unavailable, numerous trials must be done and field time increases significantly.
After a road has been walked and verified, centerline flagging can be placed. Critical points such as steep slopes, cuts and fill, and wet ground are identified. If the road is going to be designed for permitting or construction contract purposes, a survey with side shot information must be done. This process is also very time consuming and is subject to errors. In addition, ground types, stream crossings, unstable terrain, spoil/waste locations, and private property boundaries are recorded.
Design and Construction Documentation
For government permitting and construction contract purposes, most forest companies in B.C. prepare a geometric road design. This design includes the following:
LiDAR-based planning consists of the same 3 phases as the Traditional Approach presented earlier: route selection, field verification and survey, and design and construction documentation. Figure 7 shows the LiDAR approach to road planning. LiDAR-based planning enhances traditional planning in several stages: (a) pre-field planning and (b) through reduced time in the field verfication stage.
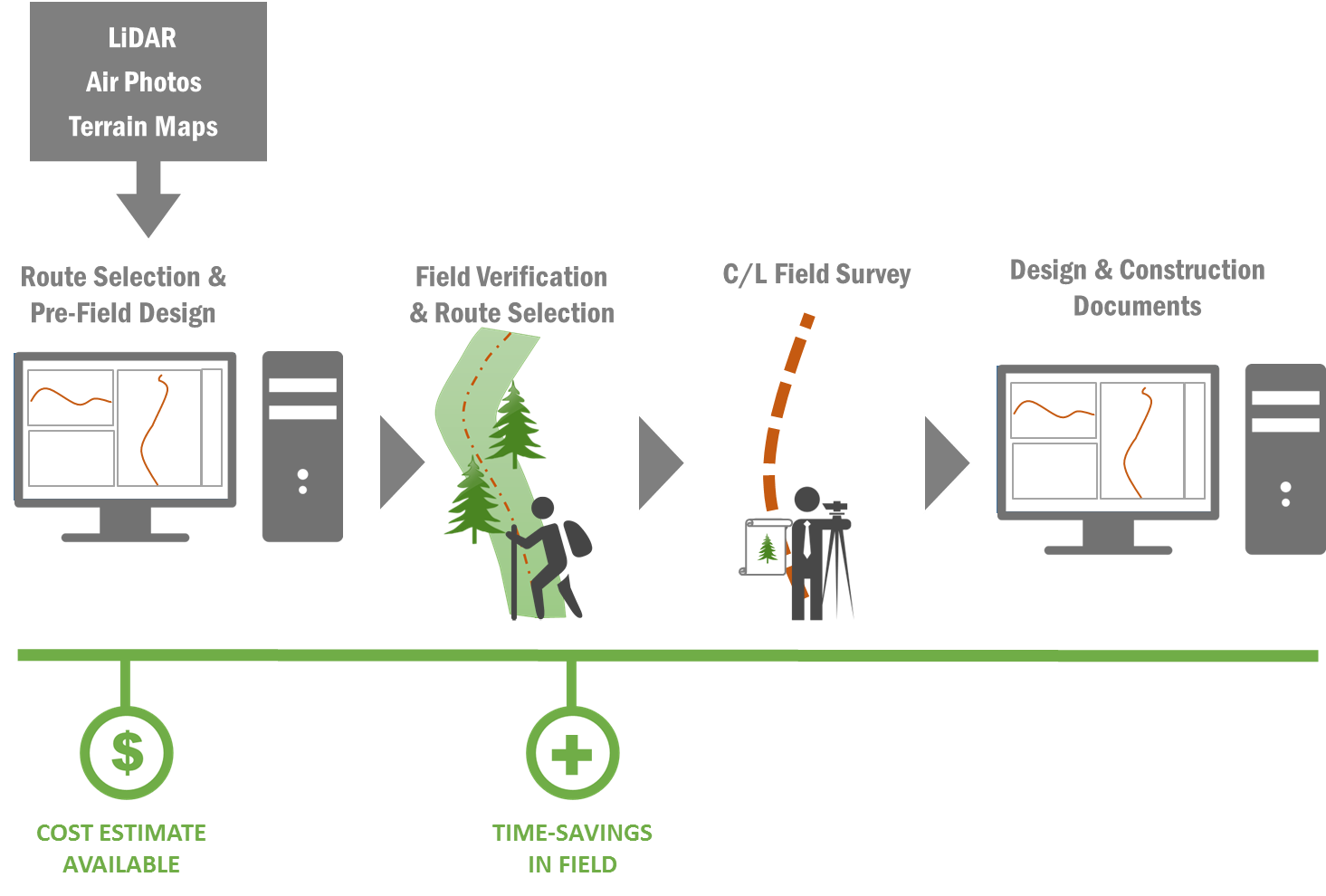
Figure 7: LiDAR-Based Approach to Road Planning
LiDAR Approach to Road Planning
Route Selection / Pre-Field Design
Using accurate LiDAR, design, costing and optimization software allows planners to quickly evaluate different alignment options. A preliminary design (Pre-Field design) is also made available before going to the field and refining the route. Instead of just pegging a road alignment, the planner can rapidly calculate and optimize cut / fill quantities, material movement, and costs. Design information such as profile and cross sections can be made available for field use. An example of this is shown in Figure 8.
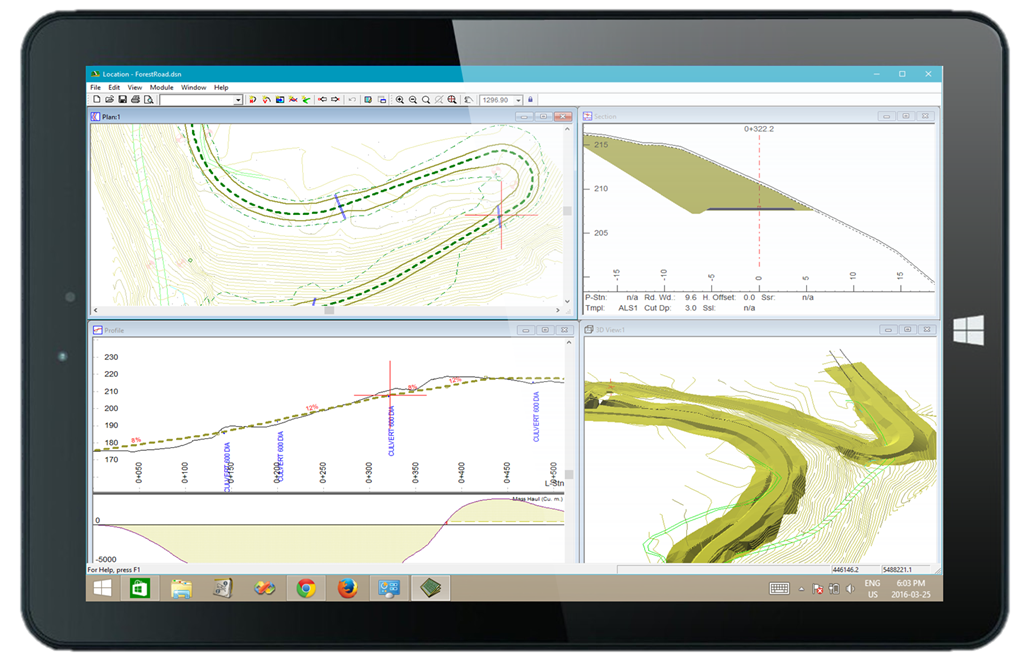
Figure 8: Geometric Design Information with Integrated GPS for Field Use
Field Verification and Survey / Reduced Field Time and Improved Survey Quality
Since the Pre-Field design has established grades, switchback locations, cut / fill and endhaul requirements, time spent re-trialing alignments in the field is reduced. In addition, survey time is reduced because only the centerline needs to be traverse-flagged. The side shot information from the LiDAR data is usually more accurate than a typical (compass and clinometer) forest road survey.
Conclusion
Due to decreasing acquisition costs and increasing availability, LiDAR is now commonly used for forest road planning and design. The benefits of this are reduced engineering time and lower construction costs due to improved road planning. LiDAR allows more design work to be done in the office prior to going to the field. It also allows planners to explore more options.
Also, by shifting more planning to the office design, field time is reduced as less reconnaissance is required. Since side shot information is available from the LiDAR, the surveying workload is reduced and accuracy is increased.
Optimization software compliments LiDAR by allowing engineers to quickly evaluate different options and their associated costs. By automating the design process, engineers can quickly minimize cuts and fills for a chosen corridor.
References
Akay, AE 2003, Minimizing Total Cost of Construction, Maintenance and Transportation Costs with Computer-Aided Forest Road Design, PhD Thesis, Oregon State University.
Conn, AR, Scheinberg, K, & Vicente, LN 2009, Introduction to Derivative-Free Optimization, IBM, Yorktown Heights, New York.
Davis, R 2002, Forest Road Engineering Guidebook, pp. 3-34, Forest Practices Board, British Columbia.
D'Eon, S 2015, ‘Better, Faster, Cheaper: Airborne LiDAR and Enhanced Forest Inventory taking off across Canada’, Logging and Sawmilling Journal, November 2015.
Ghaffariyan, M, Stampfer, K, Sessions, J, Durston, T, Kuehmaier, M, & Kanzian, CH et al, 2010, ‘Road Network Optimization using Heuristic and Linear Programming’, Journal of Forest Science.
Hare, W, Hossain, S, Lucet, Y, & Rahman, F 2014, ‘Models and strategies for efficiently determining an optimal vertical alignment of roads’, Computers & Operations Research.
Hugelschaffer, 2004, ‘Use of LiDAR in Forestry Applications’, proceedings from the LiDAR workshop hosted by Sunpine Forest Products, British Columbia, 24 March.
Leboeuf, A 2015, Province Wide Data Acquisition, Impact analysis and recommendations, Province of Quebec, Quebec.
Reutebuch, SE 1988, ‘ROUTES: A Computer Program for Preliminary Route Location.’ General Technical Report, Pacific Northwest Research Station: U.S. Department of Agriculture, Forest Service. Available from: Treesearch digital library [PNW-GTR-216].
Rogers, L & Schiess, P 2001, ‘Pegger and Roadview: A New Tool to Assist Engineers in Operation Planning’, proceedings from the International Mountain Logging and 11th Pacific Northwest Skyline Symposium, Seattle WA, 10-12 December.
Sessions, J 1992, ‘Using network analysis for road and harvest planning’, proceedings from the workshop on Computer Supported Planning of Roads and Harvesting, 26–28 August.
Sessions, J 1978, ‘A heuristic algorithm for the solution of the variable and fixed cost transportation problem’, proceedings the 1985 Symposium on System Analysis in Forest Resources, Athens, University of Georgia.
Softree Technical Systems 2015, ‘LiDAR Usage Customer Survey’, online survey, collected with Survey Monkey [March 9 2015].
Softree Technical Systems 2016, Softree Optimal for RoadEng Version 7, software program, Softree Technical Systems, North Vancouver, British Columbia.
Stueckelberger, J, Heinimann, HR, Chung, W, & Ulber, M 2006, ‘Automatic road-network planning for multiple objectives’, in proceedings of the 29th COFE Meeting, Coeur d’Alene, Idaho, 30 July to 2 August. Edited by Chung, W, & Han, HS.
Tan, J 1999, ‘Locating forest roads by a spatial and heuristic procedure using microcomputers’, International Journal of Forest Engineering, pp. 91–100.